- Pengurutan Berdasarkan Penyisipan (Insertion Sort)
Idenya adalah mencari tempat yang tepat untuk setiap elemen tabel, dengan cara sequential search,
kemudian setiap kali menyisipkan satu elemen tabel yang diproses ke tempat yang seharusnya.
Proses dilakukan sebanyak N tahapan (yang dalam sorting disebut sebagai “Pass”). Pada setiap Pass, tabel terdiri dari dua bagian : yang sudah terurut yaitu [1…..Pass-1], dan sisanya
[Pass..Nmax] yang belum terurut. Ambil elemen TabInt(Pass), sisipkan ke dalam TabInt[1..Pass-1]
dengan tetap menjaga keterurutan. Untuk menyisipkan TabInt(Pass) ke TabInt(i) harus terjadi
pergeseran elemen tabel TabInt[1..Pass]. Pergeseran ini dapat dilakukan sekaligus dengan pencarian i. Pencarian dapat dihentikan segera dengan memanfaatkan sifat keterurutan
TabInt[1..Pass].
Metoda pengurutan ini cukup efisien (≅N) terutama untuk N yang kecil. Pencarian dengan sentinel dapat dimanfaatkan pada Insertion Sort. Pada kasus ini, sentinel
ditaruh pada TabInt(0) karena pada tahapan ke-Pass, pencarian berurutan dilakukan pada
TabInt[Pass-1..1]
Contoh program pengurutan data barang menggunakan metoda Insertion Sort
hasil running nya adalah :
- Pengurutan Berdasarkan Pertukaran Harga (Bubble Sort)
Idenya adalah gelembung air yang akan mengapung : elemen berharga kecil akan “diapungkan”,
artinya diangkat ke atas melalui pertukaran. Proses dilakukan sebanyak N tahapan (yang dalam
sorting disebut sebagai “Pass”). Pada setiap Pass, tabel terdiri dari dua bagian : bagian yang sudah
terurut yaitu [1..Pass-1] dan ide dasarnya adalah mengapungkan elemen ke-Pass sampai pada
tempatnya.
1. Untuk setiap dua elemen suksesif TabInt(K) dan TabInt(K-1), K[2..N], TabInt(K-1) <=
TabInt(K), dengan demikian TabInt(K) harus ditukar dengan TabInt(K-1) jika sifat di atas
tidak dipenuhi. Karena dilakukan secara berurutan, TabInt(1) berisi harga terkecil
Materi Kuliah Pemrograman Terstruktur I
IF - UTAMA Versi/Revisi : 1/0 Halaman : M-IX/X-17
2. Untuk setiap dua elemen suksesif TabInt(K) dan TabInt(K-1), K[3..N], TabInt(K-1) <=
TabInt(K), dengan demikian TabInt(K) harus ditukar dengan TabInt(K-1) jika sifat di atas
tidak dipenuhi. Karena dilakukan secara berurutan, TabInt[1..2] terurut.
3. Untuk setiap dua elemen suksesif TabInt(K) dan TabInt(K-1), K[4..N], TabInt(K-1) <=
TabInt(K), dengan demikian TabInt(K) harus ditukar dengan TabInt(K-1) jika sifat di atas
tidak dipenuhi. Karena dilakukan secara berurutan, TabInt[1..3] terurut.
………………….
N-1. Untuk setiap dua elemen suksesif TabInt(K) dan TabInt(K-1), K[N-1..N], TabInt(K-1) <
TabInt(K), dengan demikian TabInt(K) harus ditukar dengan TabInt(K-1) jika sifat di atas
tidak dipenuhi. Karena dilakukan secara berurutan, TabInt[1..N] terurut.
TabInt[1..N] sudah terurut : TabInt(1) <= TabInt(2) <= TabInt(3) <= ….<= TabInt(N)
Kamus :
i, K : integer{indeks untuk traversal tabel}
Pass : integer{tahapan pengurutan}
Temp : integer{Memorisasi untuk pertukaran harga}
Sebetulnya proses dapat dihentikan jika tidak terjadi pertukaran. Manfaatkan sifat ini dengan
memekai sebuah besaran boolean, dan tuliskanlah algoritmanya untuk memperoleh versi yang
optimum. Versi asli metoda ini biasanya paling diingat karena prinsipnya yang “alamiah”, tapi
performansinya tidak bagus (kecuali versi yang sudah dibuat efisien), maka tidak
direkomendasikan untuk dipakai.
Contoh program pengurutan data barang menggunakan metoda Bubble Sort








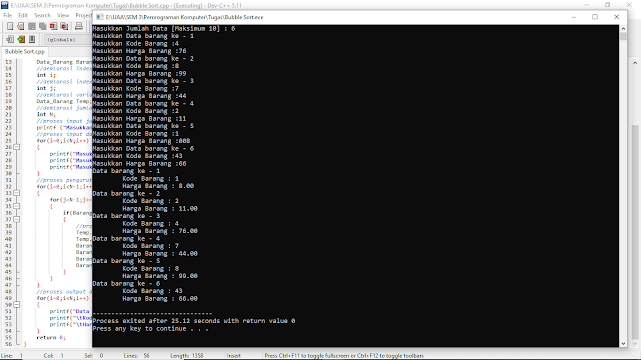








.webp)


.webp)

0 komentar